The difficulty of dendritic inhibition: Trading off accumulative inhibition and chloride loading
In reference to paper: Currin, Christopher Brian, and Joseph Valentino Raimondo. “Computational Models Reveal How Chloride Dynamics Determine the Optimal Distribution of Inhibitory Synapses to Minimise Dendritic Excitability.” PLOS Computational Biology 18, no. 9 (September 23, 2022): e1010534. https://doi.org/10.1371/journal.pcbi.1010534
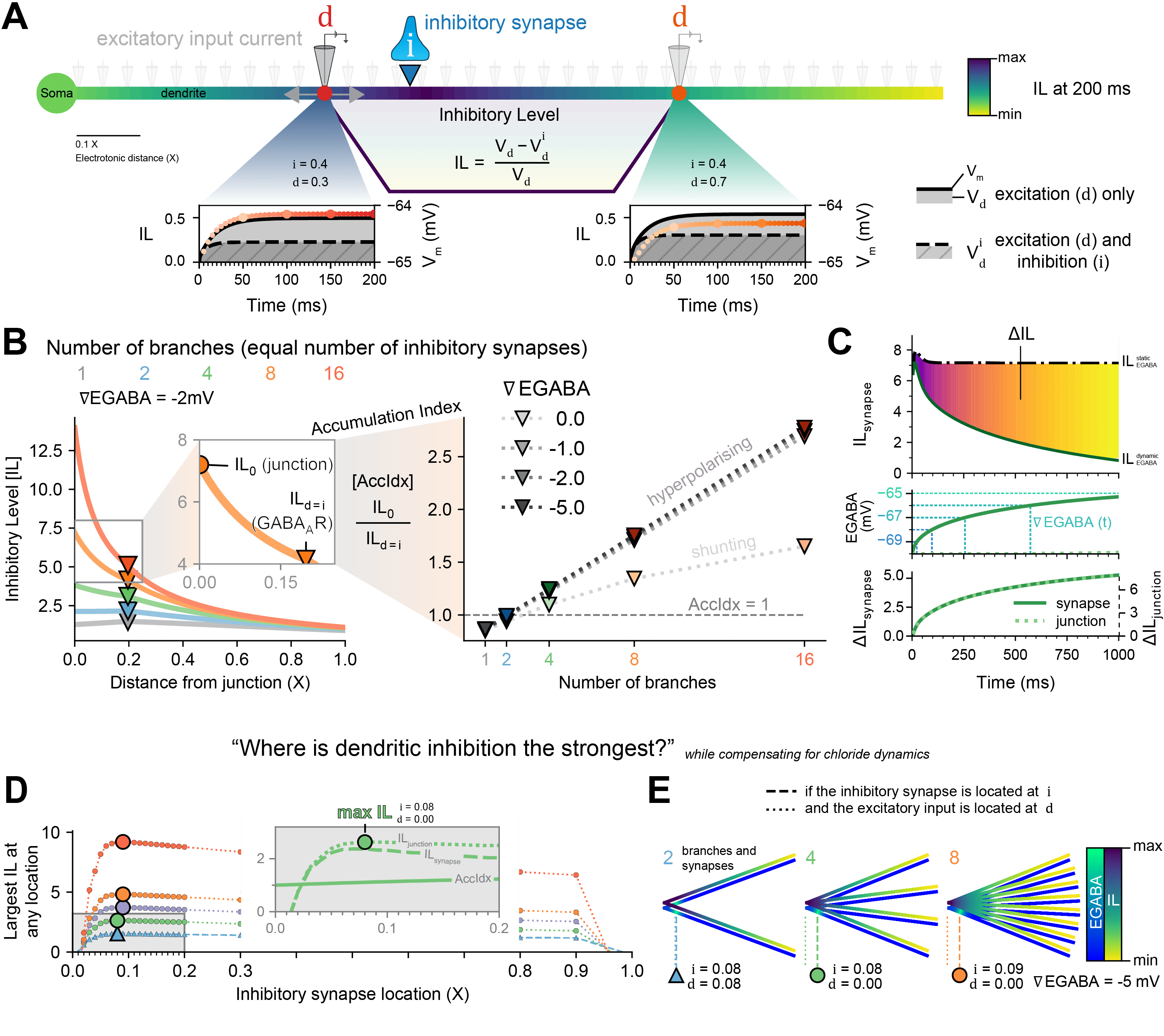
Figure 1: The Inhibitory Level as a metric to answer, “Where is inhibition the strongest?”, while compensating for chloride (Cl-) dynamics. (A) The effect an inhibitory synapse at i would have on excitatory input at d is reflected in the area-difference between the membrane potential (Vm) with only excitation and the Vm with excitation and inhibition. (B) The IL is dependent on the number of branches (with an equal number of inhibitory synapses) and ∇EGABA but the Accumulation Index (AccIdx) is only dependent on the number of branches and not ∇EGABA, for hyperpolarising synapses. (C) IL at the synapse and at the junction increase over time as EGABA becomes less hyperpolarised, but in proportion. (D) The optimal location of inhibitory synapses was explored in dendrites with 2 or more branches and with dynamic Cl-. (E) The maximum IL (yellow-purple heatmap) was at the synapse itself for 2 branches but at the junction with more branches, with inhibitory synapses located a short distance away from the junction in order to prevent too much Cl- loading (blue-green heatmap).
Abstract
Many neurons in the mammalian central nervous system have complex dendritic arborisations and active dendritic conductances that enable these cells to perform sophisticated computations. How dendritically targeted inhibition affects local dendritic excitability is not fully understood. Here, we use computational models of branched dendrites to investigate where GABAergic synapses should be placed to minimise dendritic excitability over time. To do so, we formulate a metric we term the “Inhibitory Level” (IL), which quantifies the effectiveness of synaptic inhibition for reducing the depolarising effect of nearby excitatory input. GABAergic synaptic inhibition is dependent on the reversal potential for GABAA receptors (EGABA), which is primarily set by the transmembrane chloride ion (Cl-) concentration gradient. We, therefore, investigated how variable EGABA and dynamic chloride affects dendritic inhibition. We found that the inhibitory effectiveness of dendritic GABAergic synapses accumulates at an encircled branch junction. The extent of inhibitory accumulation is dependent on the number of branches and location of synapses but is independent of EGABA (when hyperpolarising). This accumulation occurs even for very distally placed inhibitory synapses when they are hyperpolarising – but not when they are shunting. When accounting for Cl- fluxes and dynamics in Cl- concentration, we observed that Cl- loading is detrimental to inhibitory infectiveness. This enabled us to determine the most inhibitory distribution of GABAergic synapses which is close to – but not at – a shared branch junction. This distribution balances a trade-off between the stronger combined inhibitory influence when synapses closely encircle a branch junction with the deleterious effects of enhanced Cl- loading that occurs when inhibitory synapses are co-located.
Here we demonstrate that 1) elevated [Cl-]i is sufficient to have a balanced network enter a SE-like state, 2) the model recapitulates experimental findings (Burman et al., 2019) in that SE-like activity is resistant to increases in GABAA receptor conductance (akin to benzodiazepine treatment), 3) recovery from SE can be facilitated by strong Cl- extrusion with the application of positive GABA conductance modulation, and 4) SE is driven by elevated [Cl-]i in pyramidal cells while interneuron Cl- has a minor influence. Together, these results provide clues to the mechanisms and potential therapies for status epilepticus.
The effects of inhibitory synaptic input are not just local changes in membrane potential (Vm), but also the propagation of voltage, given by the cable equation [1], and the spread of lowered input resistance along a neuron [2]. We captured both effects in something we term the “Inhibitory Level” (IL): the impact that an inhibitory synapse at a location i would have on an excitatory input at location d (Fig. 1A). The IL is dependent on the number of branches and the relative inhibitory reversal potential (∇EGABA), yet the ratio between the IL at the junction (IL0) and the IL at the inhibitory synapse (ILsynapses) – the accumulation index (AccIdx) – is independent of ∇EGABA for hyperpolarising synapses (Fig. 1B). GABAergic synapses are permeable to chloride ions (Cl-) and evidence shows that small changes in the internal Cl- concentration ([Cl-]i) can lead to large changes in activity [3]. Therefore, we sought to determine the best placement for inhibitory synapses that maximises dendritic inhibition while accounting for the influx of Cl- during inhibitory signalling (Fig. 1C). The difference in IL (ΔIL) between a simulation with and without Cl- dynamics, even as EGABA increases locally, is proportional across the dendrite (Fig. 1C). To answer the question, “Where is dendritic inhibition the strongest?”, while compensating for chloride dynamics, we moved GABAergic synapses along dendrite branches and recorded the IL everywhere (Fig. 1D and zoom). The maximum IL (Fig. 1E) for more than 2 branches was when GABAergic synapses were a short distance away from the junction (i ≈ 0.08 X) and the excitatory current was at the junction itself (d ≈ 0.0 X). This contrasts with simulations without Cl- dynamics where both are at the junction itself for the maximum IL. Our results provide a framework for understanding how Cl- dynamics affects the optimal distribution of GABAergic synapses to maximise suppression of local dendritic excitability. This work will be of interest to both computational and experimental neuroscientists interested in inhibitory synaptic transmission.
Acknowledgements
The German Academic Exchange Service or DAAD (German: Deutscher Akademischer Austauschdienst) for awarding me funding to perform research in Berlin during 2018.
Thanks to the National Research Foundation (NRF) of South Africa and the University of Cape Town for funding this research.
References
[1] Rall W. Theoretical Significance of Dendritic Trees for Neuronal Input-Output Relations (1964). In: Segev I, Rinzel J, Shepherd GM, editors. The Theoretical Foundation of Dendritic Function. Palo Alto, CA, CA: The MIT Press; 2003. doi:10.7551/mitpress/6743.003.0015 [2] Gidon A, Segev I. Principles governing the operation of synaptic inhibition in dendrites. Neuron. 2012;75: 330–341. doi:10.1016/j.neuron.2012.05.015 [3] Raimondo J V, Richards BA, Woodin MA. Neuronal chloride and excitability — the big impact of small changes. Curr Opin Neurobiol. 2017;43: 35–42. doi:http://dx.doi.org/10.1016/j.conb.2016.11.012
Topic
Dendrites,